2023寒假超算与并行计算学习汇报
汇报PPT
















分解技术与分解策略
分解技术和分解策略是并行计算中的两个相关但不同的概念。分解技术涉及到将问题划分成可以并行处理的部分,而分解策略则是指如何将这些部分分配给不同的处理器或计算资源。下面详细解释这两部分的内容:
分解技术
分解技术是并行计算中的核心概念,它决定了如何将一个大问题拆分成小问题,以便于并行处理。主要有三种分解技术:
- 域分解 (Domain Decomposition): 这种技术将整个计算域(比如一个物理空间、一个时间间隔或一个数据集)分割成若干子域。每个子域可以被单独分配给一个处理器进行计算。例如,在模拟天气系统时,可以将大气模型的不同区域分配给不同的处理器。
- 功能分解 (Functional Decomposition): 在这种技术中,不同的功能或任务被分配给不同的处理器。每个处理器执行一个特定的函数或任务,这些任务可能是并行的,也可能是顺序的。例如,在一个视频处理流水线中,一个处理器可能负责解码,另一个处理器负责渲染,再一个处理器负责压缩。
- 数据分解 (Data Decomposition): 这种技术涉及将数据集分割成较小的部分,这些部分可以独立地并行处理。例如,在处理大型数组时,可以将数组分成多个块,每个块由不同的处理器处理。
分解策略
分解策略决定了如何将分解后的任务或数据块分配给处理器。这个策略对于负载平衡、减少通信开销和提高并行效率至关重要。主要的分解策略包括:
- 块分解 (Block Decomposition): 将数据集或任务分割成大小相等的块,每个处理器处理一个或多个块。这种策略简单易于实现,但可能不够灵活以应对动态变化的负载。
- 循环分解 (Cyclic Decomposition): 数据集被分割成更小的块,并以循环的方式分配给处理器。这种方法可以提供更好的负载平衡,特别是当处理的时间难以预测时。
- 块循环分解 (Block-Cyclic Decomposition): 结合了块分解和循环分解的特点,数据集被分割成大小相等的块,然后这些块以循环的方式分配给处理器。这种策略试图平衡负载和减少通信开销。
在实际应用中,选择合适的分解技术和策略取决于问题的性质、计算资源的特点以及性能优化的目标。例如,如果处理器之间的通信成本很高,可能会倾向于选择减少通信需求的分解策略。如果任务的执行时间变化很大,那么需要一个更灵活的负载平衡策略。
在设计并行程序时,通常需要综合考虑分解技术和分解策略,以确保程序运行的效率和可扩展性。实际上,这两者是相互影响的:选择了某种分解技术后,可能会限制可用的分解策略,反之亦然。因此,开发者需要对问题和计算环境有深入的理解,才能选择最合适的方法。
分解技术
简介
设计并行算法的一个基本的步骤是描述完成给定任务所需要的计算,并把这些计算分解为可以并行执行的子任务集。对很多的问题来说,它们的任务图都包含了足够的并行性。对这样的任务图,各个任务可以在多个处理器上进行调度,从而使得问题得以并行的完成。但不幸的是,很多的问题的任务图中并不表现出如此丰富(或者称为直观)的并行性,相反的,它们往往包含一个任务或者多个需要串行执行的任务。对这样的问题,我们需要将总的计算任务进行分解为一个可以并行执行的子任务集,这个过程称为任务分解。一个好的任务分解应该具有下面的特点:
☆ 它应该有很高的并行度。并行度越高意味着这个分解后的任务可以在越多的处理器上并行的执行。
☆ 子任务间的交互(通信和同步)应该尽可能的少。交互少意味着处理器可以更专心的完成任务本身而不是其它由于通信和同步带来的额外计算和等待。
很多情况下,这两个要求会产生冲突,也就是说,有很高的并行度的任务分解,通常需要子任务间的大量交互操作。如何平衡冲突是并行算法设计中的艺术。这一节中主要考虑如何提高子任务的并行度,关于子任务间的交互的讨论在下一节进行。
下面介绍几种用于任务分解的常用的方法。对不同的问题,这些方法并不总是可行,而且也不一定会得到最有的并行算法,但对很多问题来说,这些方法可以提供一个好的并行化的”着眼点”。
其中的递归分解和数据分解可以被看成是相对通用的分解方法,因为它们可以用来对大多数的问题进行任务分解,而搜索分解要特殊一些,它只能应用于某些特定类型的问题。
递归分解技术
递归分解通常用来对采用Divide-and-conquer(分治)方法的问题进行任务分解。这种方法将任务分解为独立的子任务,这个分解的过程会递归的进行。问题的答案是所有的子任务的答案的组合。分-治策略表现出一种自然的并行性。
示例:快速排序
对n个元素的序列A进行快速排序。快速排序算法是一种分治的算法。算法首先选取一个轴元素x,然后把A分成两个子序列A0和A1,其中A0中的所有元素小于x,而A1中的所有元素大于等于x,这是算法的分割部分。对得到的子序列递归地进行上面的分割过程,然后用经过排序的子序列组合成最后的结果序列A’。快速排序的过程可以用下面的图来示例。

其中的深色的元素为选中的轴元素。
现在考虑如何根据算法的分-治特性来对快速排序算法进行任务分解。从上面的图可以看出,对任务树的每一层,每个子任务的继续分割是可以并行执行的,而且它们互相独立。因此对计算的分解实际上也是一棵树。算法开始时,只有一个序列(树的根节点),我们用一个处理器来完成对它的第一次分割。分割完成后,我们得到了第一层中的2个子序列,对这两个子序列的分割可以在两个处理器上分别进行,(如果序列足够长)树中的第i层中会出现2i个子序列,它们可以由2i个处理器独立并行完成。
数据分解技术
对那些具有大型数据结构的算法来说,数据分解是一种非常有用的方法。它可以分为两个步骤。第一个步骤中,对计算操作的数据(或称为域)进行划分,第二个步骤根据数据的划分来将对应的计算组织成相应的子任务。对数据的划分可以用下面的方法进行。
对输出数据进行划分
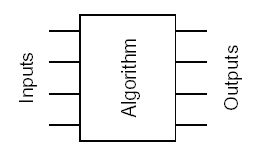
这个算法有一个输入集,经过处理后,得到一个输出集。如果输出集中的每个元素都是独立计算的,那么,对输出集的任何划分都会有一个对应的并行任务分解方案。这种分解的最大并行度等于输出集的规模。数据分解是一种很有效的发现并行性的方法。
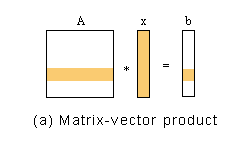
x,b是n维向量,A是一个n×n的矩阵,计算矩阵向量积如下:
b=Ax
b是算法的输出,我们来看b的每个元素是如何得到的。b的每个元素可以用下面的公式的到:
$$
b_i = a_{i1}x_1 + a_{i2}x_2 + \cdots + a_{in}x_n
$$
由于b的各元素的计算可以独立(并行)进行,我们可以将这个计算按照b的元素进行数据划分:n个处理器,每个处理器完成一个元素的计算。
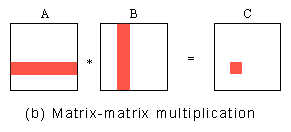
C的每个元素是A的第i个行向量与B的第j个列向量的点积,因此,可以按照C的元素进行数据划分,并把计算每个C的元素的任务作为一个子任务
对中间数据进行划分
在很多的算法中,输出集中的数据之间的存在复杂的依赖关系,这种情况下,对输出集按照元素进行划分不再可行。对有的算法来说,它们的计算可以被重新组织为下面的多级计算

其中每级的输出数据之间没有依赖关系(它们对应的计算可以并行进行)。此时可以对中间数据(每级的输出)进行数据划分。
比如下面的计算前序和的算法:
对长度为n的序列A计算前序和,结果存储在S中,计算的过程可以分为i= 个步骤,在每个步骤中,有
个步骤,在每个步骤中,有 。
。

void hillisSteeleScanParallel(int *input, int *output, int n) {
// 复制输入到输出,为前缀和计算做准备
for (int i = 0; i < n; ++i) {
output[i] = input[i];
}
// 对数步骤的Hillis-Steele算法
for (int step = 1; step < n; step *= 2) {
// 创建一个临时数组来存储这一步的计算结果
int *temp = (int *)malloc(n * sizeof(int));
if (temp == NULL) {
fprintf(stderr, "Memory allocation failed!\n");
exit(EXIT_FAILURE);
}
// 并行执行每一步的计算
#pragma omp parallel for
for (int i = 0; i < n; ++i) {
if (i < step) {
temp[i] = output[i];
} else {
temp[i] = output[i] + output[i - step];
}
}
// 将临时数组复制回输出数组
for (int i = 0; i < n; ++i) {
output[i] = temp[i];
}
// 释放临时数组的内存
free(temp);
}
}对输入数据进行划分
前面讨论的两种数据划分方法实际上都是对输出数据进行划分,能进行这种划分的一个前提是每个输出都可以被自然的表示为输入数据的函数。对很多算法,这个条件并不一定能满足,比如对一个排序算法,输出的每个元素的位置不能被(有效的)独自确定。这种情况下,由于无法对输出数据进行划分,有时可以尝试对输入数据进行划分,然后根据这个划分来得到并行任务集。每个并行子任务在(自己的)数据(或称为本地数据)上进行尽可能多的计算。需要注意的是,这些并行任务集给出的计算结果也许还不是原来问题的答案,因此,常常还需要一个计算阶段来根据这些结果来生成最后的答案。
考虑前面讨论过的快速排序算法。快速排序算法一个重要步骤是选定一个序列中的一个元素作为轴元素(pivot),然后对序列进行划分,划分后一个子序列包含所有比轴元素小的元素,而另外一个子序列包含比轴元素大(或等于)的元素。现在考虑如何来完成这个步骤。假设序列是一个n个元素的数组,为了简化讨论,我们假设挑选的轴元素在数组中是唯一的(即它的值与其它的数组元素的值都不同)。下面的图给出了一个实例(n=16)。5被选为轴元素(这个选择本身所用的算法我们在此不做讨论)。左边是算法输入,右边是算法输出(都是一个单一的数组)。现在考虑这个问题的解决方法。为了得到结果序列,输入数组的每个元素需要和轴元素进行(独立的)比较,然后需要计算出比轴小的元素的数目以及比轴大的元素的数目,这样,轴元素在输出数组中位置(数组下标)就确定了,其余的元素可以很简单的从输入数组拷贝到输出数组。
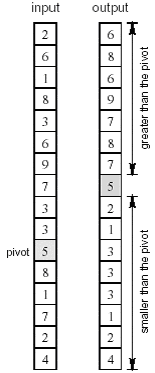
上面的算法不可能使用对输出数据进行划分的方法:因为输出序列中的每个元素的下标不能根据输入序列(注意,有可能,但并不高效)单独计算。但这个算法可以通过对输入数据划分的方法来开发并行性。这种划分的细节可以参考下面的图。16个元素的数组被均匀的划分成4个子序列(以分配给4个处理器并行处理)。
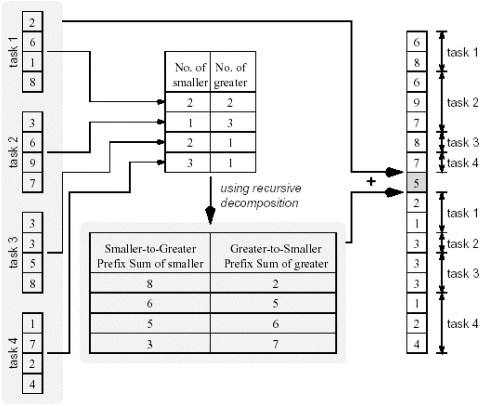
算法包括三个阶段。第一阶段每个处理器将自己的序列中的各元素与轴元素进行比较,得到本地序列中比轴元素小的元素数目和大于等于轴元素的元素数目。第二个阶段中采用递归分解的方法来对上面的数据计算前序和(注意计算小元素数目和大元素数目的方向不同)。第三个阶段中每个处理器根据自己本地的前序和(实际上给出了输出数组的下标),来将本地的元素拷贝到输出数组中。
对有的算法,虽然可以采用按输出数据进行划分的方法,但在此基础上对输入数据进行划分也许可以提供额外的并行化途径。考虑下面的例子:计算一个事务数据库中某个项目集出现的频率。事务集T包含n个事务,项目集I包含m个子项目集(I= I1,I2,…,Im)。每个事务和项目集由一些项目组成,这些项目都包含在一个可能项目集M中。计算的输出是对每个项目集Ii,计算出它在所有的事务中出现的总次数。下面的图给出了一个计算的实例。
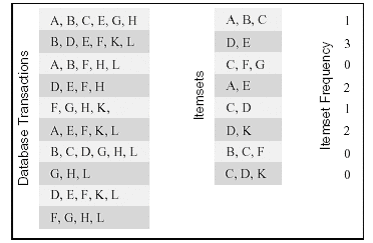
这个例子中数据库包括10个事务,而我们感兴趣的项目集有8个,计算结果为每个项目集在事务中出现的总次数。比如,项目集{D,E}在事务{B,D,E,F,K,L},{D,E,F,H},{D,E,F,K,L}中出现,所以,它的出现频率为3。
实际上,这种类型的计算是数据挖掘问题的一个必需的步骤,称为关联规则发现(association rule discovery)。解决这个问题的串行算法会为I中的子项目集建立一个查找结构(比如哈希树),然后对T中的每个事务,它会穷举所有的可能的项目组合,看能否和I中的任何项目集相匹配。比如,对于事务{A,B,C},算法可能构造的项目集包括{A},{B},{C},{A,B},{A,C},{B,C},{A,B,C}(实际上是事务的幂集除去空集),然后看它们是否在查找结构中存在。如果找到一个匹配,就把对应的频率计数器加1。使用查找结构的目的是为了使匹配的过程更加高效。
在这个算法中,有两个输入T,I和一个输出数组。它们都可以用来对算法进行划分。比如,我们可以对T进行划分:把它分成两个相同大小的子集,分别进行计算,然后对最后的结果进行组装。如下图所示:
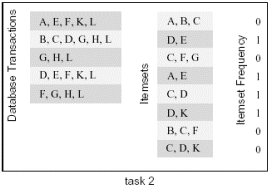
另外一种可行的数据划分方法是对项目集I进行划分:把I划分为两个相同大小的部分,它们可以独立的计算出自己的频率。(需要注意的是,对输出数据进行划分的结果和这种划分得到的结果相同,因为项目集和频率是一一对应的关系)。
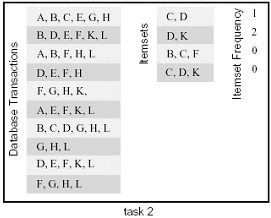
数据划分小结
一般的来说,当我们需要决定对数据如何划分或者是对那些数据进行划分时,我们需要看哪一种划分能够得到一个最好的(或者最简单的)计算划分。因为数据划分的目的只不过是为了得到一种合理的计算划分。对有些问题来说,对输入数据进行划分效果比较好,而对有些问题,对输出数据(计算结果)进行划分要更好一些。在使用数据分解的时候,需要对所有可能的数据划分方式进行考察。
拥有者计算规则(The Owner-compute Rule)
上面介绍的方法都偏重于介绍如何对数据进行划分以及选择什么样的数据进行划分,但既然我们需要的得到的是计算划分,因此,如何从数据划分得到一个计算划分是这种并行性开发的一个必需的步骤。事实上,上面的例子都采用了一种”拥有者计算规则”来从一个数据划分得到相应的计算划分。基本思想是每个计算划分完成对它所拥有的数据的全部计算。当然,对不同的数据特点以及用于进行数据划分的数据的不同类型,拥有者计算规则也许意味着不同的含义。比如,当我们采用输入数据进行划分时,拥有者计算规则代表我们使用这些输入数据(经过划分的数据)可以进行的所有计算。而对于输出数据划分,拥有者计算规则则表示生成这些数据所需要的所有计算。
分解策略
高性能计算(High-Performance Computing, HPC)中的分解策略通常涉及将大型的计算任务分解成小块,这样可以在多个处理器上并行执行,以提高计算效率。以下是三种常见的分解策略:
块分解(Block Decomposition):
介绍:块分解通常用于数据分区,将数据集分割成较小的、相等大小的块,每个处理器或核心处理一个或多个数据块。
适用范围:适用于数据可以独立处理的情况,例如在矩阵运算或图像处理中常用。
块分解示例
int remainder = n % world_size;
for (int i = 0; i < world_size; i++)
{
counts[i] = n / world_size + (i < remainder ? 1 : 0);
displacements[i] = (i > 0) ? (displacements[i - 1] + counts[i - 1]) : 0;
}循环分解(Cyclic Decomposition):
介绍:循环分解是将循环迭代分配给不同的处理器,通常是以轮询的方式。例如,如果有4个处理器,处理器1得到所有形式为4n+1的迭代,处理器2得到形式为4n+2的迭代,以此类推。
适用范围:这种方式适用于迭代次数多,但每次迭代计算量小的场景。循环分解适合那些具有大量独立迭代且每次迭代的计算量相对均匀的循环,这样可以在多个处理器之间实现有效的负载均衡
循环分解示例
int rank, size;
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Comm_size(MPI_COMM_WORLD, &size);
n_iterations = 100; // 假设我们有100次迭代
// 循环分解
for (i = rank; i < n_iterations; i += size) {
// 在这里执行每次迭代的工作
// rank表示当前进程编号,i表示迭代索引
printf("Processor %d is doing iteration %d\n", rank, i);
// ... 进行计算 ...
}
MPI_Finalize(); // 结束MPI环境
return 0;块循环分解(Block-Cyclic Decomposition):
介绍:块循环分解是块分解和循环分解的结合。数据被分成块,但分配给处理器的方式是循环的。这种方法既可以保持负载均衡,又可以减少通信开销,
适用范围:适用于处理器之间的数据交换较多的情况。
块循环分解示例
int rank, size;
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Comm_size(MPI_COMM_WORLD, &size);
int rows_per_process = MATRIX_SIZE / size; // 每个进程处理的行数
int remaining_rows = MATRIX_SIZE % size; // 剩余的行数
// 分配额外的行
if (rank < remaining_rows) {
rows_per_process++;
}
for (int block_start = 0; block_start < rows_per_process; block_start += BLOCK_SIZE) {
// 处理当前块
process_block(start_row, end_row, rank);
}其他知识点
void*自动转换数据类型
在 C 语言中,malloc 函数的返回类型是 void*,它是一种通用指针类型,可以被转换为任何其它类型的指针,而不丢失信息。在 C 标准中,void* 类型的指针可以自动地、隐式地转换为其它类型的指针。
因此,在 C 语言中,下面的代码:
int *counts = malloc(sizeof(int) * world_size);是完全有效的,因为返回的 void* 类型的指针会自动转换为 int* 类型的指针。编译器会在编译时进行这种转换,不需要显式地进行类型转换。
然而,在 C++ 中,这种隐式转换是不允许的。如果你在 C++ 代码中使用 malloc,你需要显式地进行类型转换:
int *counts = (int *)malloc(sizeof(int) * world_size);但是在 C++ 中,通常不推荐使用 malloc 和 free,而是推荐使用 new 和 delete 操作符,因为它们支持构造和析构函数的调用,这是 malloc 和 free 所不具备的。
总的来说,在 C 语言中,你的代码是没有问题的,不需要显式转换。但是,如果你的代码需要在 C++ 环境下编译,那么你需要添加类型转换,或者更好的是,使用 C++ 的内存分配方法。
什么时候自动转换数据类型
在 C 语言中,void* 类型的指针可以自动转换为其他任何类型的指针,这种转换是隐式的,不需要程序员显式进行类型转换。这是 C 语言的一个特性,它允许灵活的指针操作。
以下是几种情况,其中 void* 指针会自动转换:
- 赋值给其他指针类型:
当你将一个void*指针赋值给另一个指针类型时,转换是自动的。
void* vptr = ...;
int* iptr = vptr; // 自动转换为 int* 类型- 作为函数参数:
当你将void*指针传递给接受特定类型指针的函数参数时,转换也是自动的。
void some_function(int* ptr);
void* vptr = ...;
some_function(vptr); // 自动转换为 int* 类型- 从函数返回:
如果函数返回类型是非void*类型的指针,那么从函数返回void*类型的指针时,也会自动转换。
int* some_function() {
void* vptr = ...;
return vptr; // 自动转换为 int* 类型
}然而,以下情况需要显式转换:
- 当编译器需要类型信息时:
例如,当你需要通过指针访问结构体成员时,你必须将void*指针转换为正确的类型。
typedef struct {
int a;
} MyStruct;
void* vptr = ...;
int value = ((MyStruct*)vptr)->a; // 需要显式转换来访问成员- 在 C++ 中:
在 C++ 中,void*指针不会自动转换为其他类型的指针,必须显式进行转换。
void* vptr = ...;
int* iptr = static_cast<int*>(vptr); // C++ 需要显式转换- 在涉及指针算术的地方:
void*指针不能直接用于指针算术,因为void类型的大小未定义。在这种情况下,你需要将void*转换为另一种指针类型,如char*,因为char的大小是确定的(1 字节)。
void* vptr = ...;
vptr = (char*)vptr + 1; // 需要显式转换为 char* 来进行指针算术在 C 语言中,通常你不需要显式地从 void* 转换到其他指针类型,除非你进行的操作需要知道指针指向的数据类型的具体大小或类型信息。在 C++ 中,你总是需要显式地进行转换。

